|
Пусть 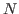 - множество натуральных чисел, - множество натуральных чисел, 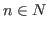 и и
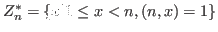 множество натуральных чисел, меньших чем множество натуральных чисел, меньших чем 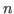 и взаимно простых с и взаимно простых с 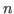 . .
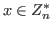 называется квадратичным вычетом по модулю называется квадратичным вычетом по модулю 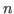 , если существует такой , если существует такой 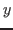 , что , что
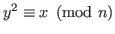 . В противном случае, . В противном случае,
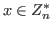 называется квадратичным невычетом по модулю называется квадратичным невычетом по модулю 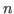 . .
Пусть 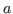 — целое число, и — целое число, и 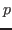 — простое число, отличное от — простое число, отличное от 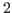 . Символ Лежандра . Символ Лежандра
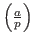 определяется следующим образом: определяется следующим образом:
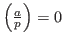 , если , если 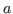 делится на делится на 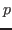 ; ;
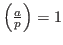 , если , если 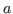 является квадратичным вычетом по модулю является квадратичным вычетом по модулю 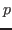 , то есть , то есть 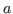 не делится на не делится на 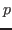 и существует такое целое и существует такое целое 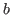 , что , что
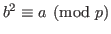 ; ;
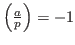 , если , если 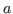 является квадратичным невычетом по модулю является квадратичным невычетом по модулю 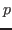 , то есть , то есть 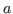 не делится на p и не является квадратичным вычетом по модулю не делится на p и не является квадратичным вычетом по модулю 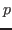 . .
Пусть 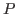 — нечётное, большее единицы число и — нечётное, большее единицы число и
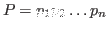 — его разложение на простые множители (среди — его разложение на простые множители (среди
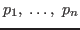 могут быть равные). Тогда для произвольного целого числа могут быть равные). Тогда для произвольного целого числа 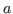 символ Якоби определяется равенством: символ Якоби определяется равенством:
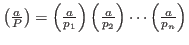 , ,
где
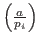 — символы Лежандра. — символы Лежандра.
По определению считаем, что
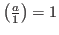 для всех для всех 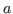 . .
Пусть 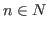 и и
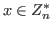 . Пусть . Пусть 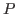 знает, что не существует такой знает, что не существует такой 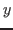 , что , что
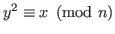 . . 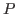 хочет доказать хочет доказать 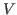 свое знание, не показывая само доказательство несуществования. свое знание, не показывая само доказательство несуществования.
|